17.11.2022

Systematische Fehler und ihre Korrektur mit Hilfe einer intelligenten Residuenquadratsumme

Dr. Thomas G. Mayerhöfer , Dr. Susanne Pahlow, Prof. Jürgen Popp, Leibniz-Institut für Photonische Technologien (IPHT)

Das A und O in der Analytik ist es, den wahren Wert einer Messgröße zu ermitteln. Messungen sind jedoch generell fehlerbehaftet, wobei man im Allgemeinen zwischen zwei Arten von Fehlern unterscheidet, die zufälligen und die systematischen Fehler. Erstere sind, wie der Name impliziert, zufällig um den a priori unbekannten wahren Wert einer Messgröße verteilt.

Gäbe es nur diese Art von Fehlern, könnte man sich diesem wahren Wert theoretisch dadurch immer mehr annähern, indem man eine immer größere Anzahl von Messungen vornimmt. Im Gegensatz dazu ist das bei systematischen Fehlern nicht möglich. Diese führen zu Abweichungen zwischen wahrem Wert und Mittelwert und sind unabhängig von der Anzahl der Messungen.

Oftmals bestimmt man nicht nur einen Messwert, sondern nimmt eine Reihe von Messwerten auf. Diese Bestimmung kann parallel und/oder sequenziell erfolgen. Ein Beispiel für eine parallele Messung ist die Aufnahme eines Spektrums, wobei die Intensität des Detektorsignals in Abhängigkeit von der Frequenz oder der Wellenzahl des Lichts bestimmt wird. Die Aufnahme eines solchen Spektrums kann zusätzlich sequenziell erfolgen, beispielsweise um den Verlauf einer Reaktion zu beobachten oder um die Zusammensetzung eines Produktes "inline" zu überwachen.

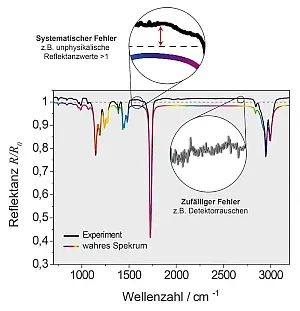
Abb.1: Darstellung typischer systematischer und
zufälliger Fehler am Beispiel eines IR-Spektrums
von PMMA auf einer Goldschicht.

Ein bekannter zufälliger Fehler, der dabei auftreten kann, ist z.B. das Detektorrauschen, wie in Abbildung1 gezeigt. Dieses lässt sich dadurch vermindern, dass mehrere Messungen direkt hintereinander durchgeführt werden und das resultierende Spektrum als das Durchschnittsspektrum aller Messungen berechnet wird. Dabei geht man davon aus, dass sich in diesem Zeitraum die Probe und die Messbedingungen, und damit das wahre Spektrum, nicht verändern.

Falls wir die Aufnahme von FT-IR Spektren betrachten, sind die Messbedingungen normalerweise über einige Minuten hinreichend konstant. Misst man allerdings über mehrere Stunden hinweg, dann kann eine Änderung der Messbedingungen dazu führen, dass sich das Hintergrund- oder Referenzspektrum ebenfalls verändert. Manchmal kann sich auch das Spektrum einer Probe selbst ändern, wenn die Probe beispielsweise nicht ausreichend equilibriert ist. Solche systematischen Fehler können etwa bei Proben auftreten, die aus dünnen Schichten auf stark reflektierenden Substraten bestehen. Sie lassen sich oft leicht detektieren, da sie zu Reflektanzen größer 1 (siehe Abbildung 1) führen, welche physikalisch unmöglich sind.

Ein weiteres Beispiel aus unserer eigenen Laborpraxis sind ATR-Spektren von Wasser. Diese können dazu benutzt werden, den Polarisationszustand der ATR-Messung zu bestimmen, wenn man die optischen Konstanten des Wassers kennt. Wiederholt man solche Messungen an anderen Tagen, so unterscheiden sich die resultierenden Spektren, bzw. deren Reflektanz generell um einen konstanten Faktor, was letztendlich großen Einfluss auf den so bestimmen Polarisationswinkel hat. Leider können moderne ATR-Einrichtungen oftmals nicht mit einem Polarisator versehen werden. Spektren, die aber nicht entweder mit parallel oder senkrecht polarisierten Licht aufgenommen werden, zeigen naturgemäß größere Abweichungen vom Beerschen Gesetz als solche, bei denen ein Polarisator zum Einsatz kommt. Deswegen ist eine auf Wellenoptik basierende Korrektur anzuraten. Generell ist dementsprechend die Vermeidung von systematischen Fehlern nicht nur eine Frage der Kosten, sondern des Kosten-Nutzen Verhältnisses.

Zur Auswertung von Spektren gibt es, wie bei anderen analytischen Techniken auch, eine ganze Reihe von Verfahren. So ist die Auftragung von Peak-Werten in Abhängigkeit von der molaren Konzentration für die quantitative Bestimmung von Analyten eine gebräuchliche Methode. Für sehr geringe Konzentrationen kann damit, wie generell bekannt, erfolgreich die Konzentration einer Lösung bestimmt werden. Weitaus weniger bekannt ist, dass dieses Verfahren für höhere Konzentrationen zu größeren Fehlern führen kann. Dies ist selbst dann der Fall, wenn die Änderung chemischer Wechselwirkungen keine Rolle spielt, da es trotzdem zu Verschiebungen der Peak-Maxima mit entsprechendem Einfluss auf die Berechnung der Konzentration kommt.[1] Stärkere lokale elektrische Felder führen zu größeren Intensitäten und Bandenflächen und offensichtlich nichtlinearem Verhalten. Ermittelt wurden diese gemäß der Lorentz-Lorenz/Clausius-Mossotti Theorie, die darauf beruht, dass Licht Materie polarisiert. So wird näherungsweise berechnet, um wie viel größer dadurch die elektrische Feldstärke des Lichtes innerhalb von Materie im Vergleich zur Feldstärke des eingestrahlten Lichtes wird.

Für solche nichtproportionalen Änderungen haben wir ein Verfahren entwickelt, welches die Korrektur systematischer Fehler erlaubt, sofern die grundlegenden dahinterliegenden Mechanismen bekannt sind und durch ein physikalisches Modell beschrieben werden können. Im Folgenden wird diese Methode am Beispiel der Dispersionsanalyse erklärt:

Die Dispersionsanalyse ist ein, heutzutage leider weitgehend unbekanntes, Werkzeug zur Spektrenauswertung. Sie ist der Vorläufer des weit verbreiteten "band fittings", bei dem Spektren mit einzelnen Lorentz- oder Gauß-Banden angepasst werden.[2] Während letzteres auf der Lambert-Beerschen Näherung beruht, basiert die Dispersionsanalyse auf der Dispersionstheorie in Kombination mit Wellenoptik.[3] Aufgrund der deutlich detaillierten Beschreibung der zugrunde liegenden physikalischen Phänomene, erlaubt die Dispersionsanalyse eine wesentlich exaktere Abbildung der Spektren als das herkömmliche "band fitting". Ziel der Dispersionsanalyse ist es, auf Basis des gedämpften harmonischen Oszillators in Verbindung mit einem geeigneten optischen Modell einer Probe deren Spektrum so gut wie möglich anzupassen ("anzufitten").

Was genau bedeutet dabei "so gut wie möglich"? Beim Fitten misst man die Güte der Anpassung dadurch, dass man die Abweichung an einem spektralen Punkt quadriert und diese quadrierte Abweichung aufsummiert. Die Summe nennt man Residuenquadratsumme oder oft auch Fehlerquadratsumme. Je kleiner diese Summe ist, desto besser repräsentiert das Modell das Spektrum und damit die Eigenschaften der Probe, so die generelle Meinung. Tatsächlich funktioniert dieses Verfahren strenggenommen nur dann, wenn das oder die Spektren nur zufällige Fehler aufweisen. Wenn das nicht der Fall ist, so wird das Verfahren durch Veränderung der Parameter des Modells dennoch versuchen, dieses an das systematisch verfälschte Spektrum anzupassen.

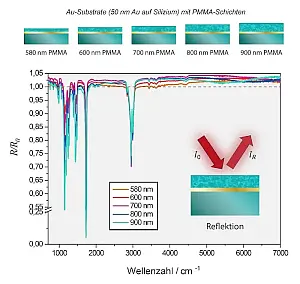
Abb.2: Unkorrigierte IR-Reflektionsspektren von
PMMA-Schichten unterschiedlicher Dicke auf
Gold-Substraten.

Nimmt man die Spektren von Schichten auf stark reflektierenden Substraten (wie in Abbildung 2 dargestellt) als Beispiel, so lassen sich diese, in Absorbanz umgewandelt und mit angepasster Basislinie, natürlich trotz unphysikalischer Reflexionswerte größer 1 problemlos anfitten, denn die Basislinienanpassung "korrigiert" den offensichtlichen Fehler. Nutzt man stattdessen die Dispersionsanalyse um das Reflexionsspektrum anzufitten, so steht man vor dem Problem, dass das darunter liegende wellenoptische Modell keine Reflexionen größer 1 zulässt. Damit lassen sich dann zumindest die schwächeren Banden nicht mehr anpassen (siehe Abbildung 1).

Natürlich könnte man immer noch auf die Idee kommen, einfach das gemessene Spektrum durch den höchsten Reflektionswert zu dividieren. Allerdings ist der entsprechende systematische Fehler nicht konstant, sondern von der Wellenzahl abhängig. Eine bessere Alternative besteht darin, die herkömmliche Residuenquadratsumme durch eine zu ersetzen, die spektrale Ähnlichkeiten oder Korrelationen miteinbezieht und höher gewichtet als die reine Reduktion der aufsummierten quadratischen Unterschiede.

Die Idee für diese ursprüngliche "smarte Fehlerquadratsumme" basiert auf der 2D-Korrelationsspektroskopie, wie sie von Isao Noda 1989 eingeführt wurde.[4] Für diese Art von 2D-Korrelationsanalyse benötigt man eine Serie von Spektren, die durch gezielte Veränderung ("perturbation") eines Parameters erzeugt wurde. Ein einfaches Beispiel ist eine Mischung von zwei Flüssigkeiten mit unterschiedlichem Dampfdruck. Nimmt man davon in regelmäßigen Abständen ein Spektrum auf, so wird dieses zunehmend von der schwerer flüchtigen Komponente dominiert. Die graphische Darstellung der Korrelationen innerhalb eines solchen Spektrensatzes als so genannte "2D maps" ermöglicht die Visualisierung von systematischen Änderungen in den Spektren, welche beim Betrachten der einzelnen Spektren nicht zugänglich wären.

Die graphische Darstellung erfolgt in zwei Teilen, dem synchronen und asynchronen Spektrum (siehe Abbildung 3). Der synchrone Part bildet die linearen/proportionalen Zusammenhänge ab, z.B. Peak A nimmt ab, während Peak B in gleichem Maße zunimmt. Der asynchrone Part hingegen visualisiert nicht-lineare/nicht-proportionale Beziehungen, wie beispielsweise Bandenverschiebungen. Mit diesem Verfahren lassen sich somit überlappende Banden elegant sichtbar machen.[5]

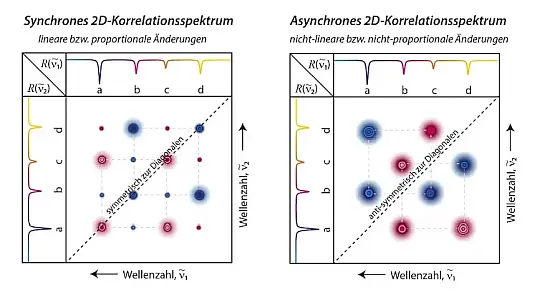
Abb.3: Schematische Darstellung synchrones und asynchrones 2D-Korrelationsspektrum.

Die 2D-Korrelationsspektroskopie ist sehr sensitiv. Mit ihrer Hilfe lässt sich auch nachweisen, dass das Beersche Gesetz auch für ideale Mischungen oder stark verdünnte Lösungen generell nicht gilt, bzw. der Zusammenhang zwischen Konzentration und Absorbanz intrinsisch nichtlinear ist.[1]

Eine Variante dieser Art von 2D-Spektroskopie entsteht dadurch, dass man ein System zwei verschiedenen Störungen unterwirft oder zwei verschiedene Spektroskopie-Arten miteinander koppelt.[5] Während in der originalen Variante das synchrone Spektrum immer symmetrisch zur Diagonalen und das asynchrone Spektrum immer antisymmetrisch zur Diagonalen ist, bestehen diese Zusammenhänge für die hybride Variante nicht mehr.

In der 2D-Korrelationsspektroskopie können auch modellierte und experimentelle Spektren miteinander verglichen werden. In diesem Fall werden diese Symmetrien zunehmend wiederhergestellt, je mehr, je besser die modellierten Spektren die gemessenen repräsentieren (siehe Abbildung 4).[6, 7]

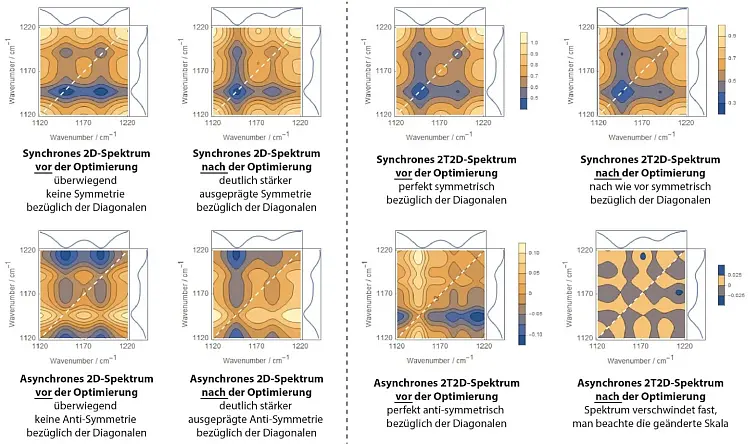
Abb.4: Vergleich der nicht optimierten mit den optimierten hybriden synchronen und asynchronen 2D-Spektren.

Mathematisch gesehen bleiben Korrelationen allerdings unverändert, wenn man beispielsweise zwei Spektren miteinander vergleicht und eines oder beide mit einem beliebigen, konstanten Faktor multipliziert. Ist dieser Faktor nicht konstant, sondern wellenlängenabhängig, so bleiben dennoch bestimmte Korrelationen zwischen den einzelnen Banden erhalten. Darauf basiert die "smarte Residuenquadratsumme".

Für die experimentelle Überprüfung dieser Idee haben wir PMMA-Schichten verschiedener Dicke auf mit Goldschichten versehenen Substraten abgeschieden und ihre MIR-Spektren aufgenommen (siehe Abbildung 2). Wie oben angemerkt, müssen sich die Spektren nichtproportional (nichtlinear) mit der Dicke ändern. Tatsächlich zeigen Schichten auf Gold sehr starke Abweichungen vom Lambert-Beerschen Verhalten.[8, 9] Aber selbst wenn man Schichten auf ein Brechungsindex adaptiertes Substrat wie CaF₂ aufbringt, führt eine Verdopplung der Dicke nicht einfach zu einer Verdopplung der Absorbanz.[10] Grund dafür sind Dispersionseffekte in Verbindung mit Interferenz.[11]

Für die Schichten verschiedener Dicke nimmt man dann an, dass sie alle dieselbe Frequenzabhängigkeit der optischen Konstanten aufweisen. Diese Frequenzabhängigkeit wird nun mittels Dispersionstheorie berechnet, wobei man einen gedämpften harmonischen Oszillator pro Peak im Spektrum annimmt. Ein solcher Oszillator ist durch drei Parameter charakterisiert, nämlich Oszillatorstärke, Position und Dämpfung. Diese drei Parameter werden nun für alle Oszillatoren so lange variiert bis die so für die verschiedenen Dicken modellierten Spektren bestmöglich mit den gemessenen Spektren übereinstimmen.[3]

Da wir allerdings wissen, dass diese Spektren systematische Fehler aufweisen, heißt in diesem Fall "bestmöglich" nicht, dass sie Punkt für Punkt übereinstimmen. Dies ist, wie oben bereits besprochen gar nicht möglich, da die experimentellen Spektren Reflexionswerte größer 1 besitzen und die wellenoptischen Beziehungen Werte größer 1 ausschließen. Stattdessen bedeutet "bestmöglich" nun, dass die modellierten Spektren so gut wie möglich mit den gemessenen Spektren korreliert sind (siehe Abbildung 5).

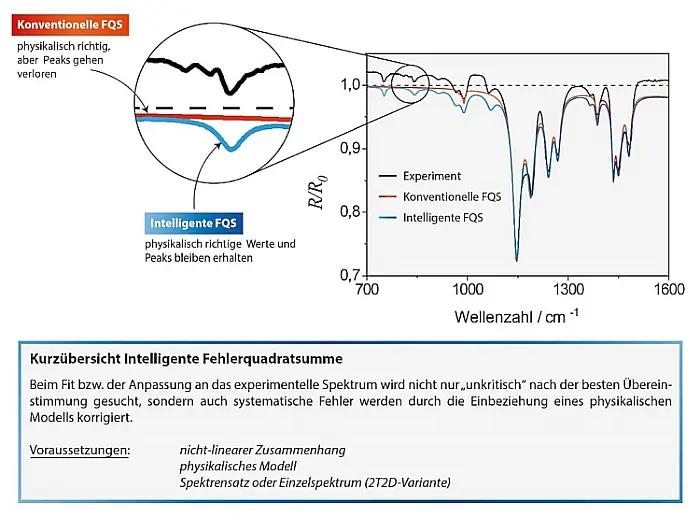
Abb.5: Vergleich der Resultate der Dispersionsanalyse eines Transflexionsspektrums von PMMA-Schichten auf Goldsubstraten
basierend auf der konventionellen und der korrelationsbasierten Fehlerquadratsumme.

Für den Fall, dass die gemessenen Spektren keine wesentlichen Fehler aufweisen, stimmen natürlich die Ergebnisse für die intelligente Fehlerquadratsumme und die konventionelle überein. Ansonsten kann die neue Methode systematische Fehler deutlich verringern und entsprechend korrigierte Ergebnisse erzielen - die simulierten Spektren stellen diese Korrektur im obigen Beispiel dar und die Oszillatorparameter entsprechen weitestgehend denen, die von Spektren ohne ersichtlichen systematischen Fehler bestimmt wurden.

Die Korrektur ist naturgemäß umso besser, je weniger stark die Frequenzabhängigkeit des Fehlers ist. Ideal ist ein multiplikativer Fehler ohne Frequenzabhängigkeit. Wo keine multiplikativen Fehler vorliegen, sondern additive kann, die neue Methode trotzdem eingesetzt werden. Additive Fehler in Absorbanzspektren verwandeln sich beispielsweise in multiplikative Fehler in Reflexions- und Transmissionsspektren. Deshalb ist die Verwendung der letzteren für die Dispersionsanalyse mit der intelligenten Residuenquadratsumme vorzuziehen.

Die neue Methode hat leider auch zwei entscheidende Nachteile. Generell liegen selten Serien von Spektren vor - viel häufiger möchte man den systematischen Fehler einer einzelnen Messung beseitigen. Darüber hinaus bedingt die hinter der smarten Fehlerquadratsumme stehende Methode, die 2D-Korrelationsanalyse, dass die Komplexität der Rechnung bzw. der Zeitaufwand mit dem Quadrat der Messpunkte bzw. der Punkte eines Spektrums anwächst. Glücklicherweise wurde vor einigen Jahren eine neue Form der 2D-Korrelationsanalyse von Isao Noda vorgestellt, bei der die Serie nur noch aus zwei Spektren bestehen muss.[12] Wir haben unsere Methode der intelligenten Fehlerquadratsumme darauf basierend so weiterentwickelt, dass nun ein Spektrum das gemessene und das zweite Spektrum das modellierte ist.[7] Damit wurde der erste Nachteil beseitigt.

Bei der Anwendung dieser neuartigen Variante erfolgt die Optimierung des Fits nicht über die Symmetrie des synchronen und asynchronen Spektrums, sondern darüber, dass das asynchrone Spektrum minimiert wird (siehe Abbildung 4, rechte Seite). Die Komplexität der resultierenden "2T2D (Two Trace 2D) smart error sum" steigt zwar weiterhin quadratisch mit der Anzahl der Messpunkte an, lässt sich aber algebraisch in eine Form überführen, deren Berechnungsaufwand nur noch linear mit der Anzahl der Punkte ansteigt, genauso wie bei der konventionellen Residuenquadratsumme.[13] Damit gibt es nur noch einen Grund die 2T2D-Residuenquadratsumme nicht anzuwenden, nämlich dass das zugrunde liegende Modell (entgegen den geforderten Voraussetzungen) linear bzw. proportional skaliert.

Gerade in der Spektroskopie scheinen Linearitäten vorherrschend zu sein. So basiert die konventionelle Chemometrie praktisch auf der Annahme, dass das Beersche Gesetz streng gültig ist.[14] Tatsächlich zeigte aber der fundamentale, aus der Maxwellschen Wellentheorie abgeleitete Zusammenhang zwischen dielektrischer Funktion und komplexem Brechungsindex ε=n² bereits vor 150 Jahren, dass die Beziehung zwischen Absorbanz und Konzentration intrinsisch nichtlinear sein muss.[15] Dabei reichen bereits kleinste Abweichungen von der Linearität um die neue Residuenquadratsumme anwendbar zu machen, denn die 2D Korrelationsspektroskopie ist ebenso wie die Hauptkomponentenanalyse sehr sensitiv gegenüber Nichtlinearitäten.[1]

Während die bisherigen Arbeiten noch sehr an die Anwendungen in der Spektroskopie angelehnt waren, nicht zuletzt wegen der Verknüpfung der 2D-Korrelationsanalyse mit dieser, haben wir inzwischen eine allgemeinere Formulierung der 2D-Korrelationsanalyse erarbeitet, die gleichzeitig eine allgemeine Anwendung der korrelationsbasierten Residuenquadratsumme einfach macht.[13]

Prinzipiell müssen in entsprechenden Programmen nur geringfügige Ergänzungen vorgenommen werden, um diese anzuwenden. Unsere aktuelle Arbeit [13] enthält dafür Skripte, die es dem Leser ermöglichen sollen, dies mit minimalem Zeitaufwand umzusetzen. Eines kann mit dem kommerziellen Programm Mathematica (Wolfram Research, Inc.) genutzt werden, während das zweite in der Programmiersprache Julia (open source) verfasst ist. So kann sich jeder Interessierte mit der Wirkungsweise der korrelationsbasierten Residuenquadratsumme vertraut machen.

Bisher ist die Arbeit lediglich als Preprint erschienen, den Code, der später als "Supporting Information" erscheinen wird, geben wir bis dahin gerne auf Anfrage weiter. In dieser Arbeit zeigen wir darüber hinaus, dass der (leicht modifizierte) Pearson-Koeffizient als korrelationsbasierte Residuenquadratsumme verwendet werden kann. Allerdings sorgen Normierungen im Vergleich zur 2T2D-Residuenquadratsumme offensichtlich dafür, dass die Fähigkeit zur Korrektur systematischer Fehler anders abgestimmt ist. Diese Unterschiede untersuchen wir aktuell.

Ein erstes Zwischenfazit ist, dass diese Unterschiede offenbar erst für größere systematische Fehler offensichtlich werden, generell aber die 2T2D-Residuenquadratsumme dem abgeänderten Pearson-Koeffizienten vorzuziehen ist.

Anwendung könnte die korrelationsbasierten Residuenquadratsumme auch für das Training von neuronalen Netzen finden. Diese nutzt man speziell zur Lösung intrinsisch nichtlinearer Probleme. Training bedeutet in ihrem Fall, dass der konkrete nichtlineare Zusammenhang zwischen Eingabedaten und Ergebnis modelliert werden soll. Der Trainingserfolg wird dabei beispielsweise über die konventionelle Residuenquadratsumme gemessen. Die korrelationsbasierte Residuenquadratsumme könnte nicht nur Fehler in den Trainingsdaten ausgleichen, sondern auch das Training erleichtern, da lineare Zusammenhänge automatisch ausgeschlossen werden.

Insgesamt sind wir sehr gespannt, in welchen Bereichen auch außerhalb der Spektroskopie die korrelationsbasierte Residuenquadratsumme Anwendung finden wird und hoffen, dass möglichst viele Wissenschaftszweige davon zukünftig profitieren werden.

Referenzen

1. T.G. Mayerhöfer, O. Ilchenko, A. Kutsyk, J. Popp, Beyond Beer's Law: Quasi-Ideal Binary Liquid Mixtures, Appl. Spectrosc., 76 (2022) 92-104.
   
2. M. Czerny, Messungen am Steinsalz im Ultraroten zur Prüfung der Dispersionstheorie, Zeitschrift für Physik, 65 (1930) 600-631.
   
3. T.G. Mayerhöfer, Wave Optics in Infrared Spectroscopy, DOI: 10.13140/RG.2.2.14293.55520, 2021.
   
4. I. Noda, Two-dimensional infrared spectroscopy, Journal of the American Chemical Society, 111 (1989) 8116-8118.
   
5. I. Noda, Y. Ozaki, Two-Dimensional Correlation Spectroscopy: Applications in Vibrational and Optical Spectroscopy, Wiley, 2005.
   
6. T.G. Mayerhöfer, M. Richard-Lacroix, S. Pahlow, U. Hübner, R. Heintzmann, J. Popp, Hybrid 2D Correlation-Based Loss Function for the Correction of Systematic Errors, Anal. Chem., 94 (2022) 695-703.
   
7. T.G. Mayerhöfer, M. Richard-Lacroix, S. Pahlow, U. Hübner, J. Popp, Smart Error Sum Based on Hybrid Two-Trace Two-Dimensional (2T2D) Correlation Analysis, Appl. Spectrosc., 0 (2022).
   
8. T.G. Mayerhöfer, J. Popp, The electric field standing wave effect in infrared transflection spectroscopy , Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 191 (2018) 283-289.
   
9. T.G. Mayerhöfer, S. Pahlow, U. Hübner, J. Popp, Removing interference-based effects from the infrared transflectance spectra of thin films on metallic substrates: a fast and wave optics conform solution, Analyst, 143 (2018) 3164-3175.
   
10. T.G. Mayerhöfer, S. Pahlow, U. Hübner, J. Popp, CaF₂: An Ideal Substrate Material for Infrared Spectroscopy?, Anal. Chem., 92 (2020) 9024-9031.
    
11. T.G. Mayerhöfer, H. Mutschke, J. Popp, The Electric Field Standing Wave Effect in Infrared Transmission Spectroscopy, ChemPhysChem, 18 (2017) 2916-2923.
    
12. I. Noda, Two-trace two-dimensional (2T2D) correlation spectroscopy - A method for extracting useful information from a pair of spectra, J. Mol. Struct., 1160 (2018) 471-478.
    
13. T.G. Mayerhöfer, I. Noda, S. Pahlow, R. Heintzmann, J. Popp, Correcting Systematic Errors by Hybrid 2D Correlation Loss Functions in nonlinear inverse modelling , Preprint, (2022).
    
14. T.G. Mayerhöfer, O. Ilchenko, A. Kutsyk, J. Popp, Infrared spectroscopy of quasi-ideal binary liquid mixtures: The challenges of conventional chemometric regression, Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 280 (2022) 121518.
    
15. T.G. Mayerhöfer, S. Pahlow, J. Popp, The Bouguer-Beer-Lambert Law: Shining Light on the Obscure, ChemPhysChem, 21 (2020) 2029-2046.

» Artikel als pdf (832 KByte)